競技プログラミングの開催サイトで有名なAtCoderで、ChokudaiSpeedRunという、典型問題ばかりを取り扱ったコンテストがあったので、基礎力をつけようと思い、解いてみた。
結果的には、C++の基本実装の学習・復習と、蟻本に載ってるような基本的なアルゴリズムの勉強になった気がする。
最大でも500点問題しかないので、（調べながら解いたが）自分にはちょうどよい難易度だった。ただ、通常のコンテストと違って解説が付いてないので、書いてみた。

A - 最大値

std::max_elementを使えば良い

// 配列の場合
int answer = *max_element(a, a+N);
// vectorの場合
int answer = *max_element(v.begin(), v.end());

B - 和

std::accumulateを使う。第三引数は初期値で、これに対して要素を順々に足し合わせていく（reduceに近い）

int answer = accumulate(v.begin(), v.end(), 0);

C - カンマ区切り

REP(i,0,N-1) cout << A[i] << ",";
cout << A[N-1] << "\n";

D - ソート

std::sortを使う。破壊的。昇順オンリー。

sort(v.begin(), v.end());

E - 1は何番目?

あえてstdを使うなら、まずstd::findで指定した値を指すイテレータを取得し、std::distanceでfirstを指すイテレータとの距離を比較することで答えを得る。

auto iterator = find(a, a+N, 1);
int answer = distance(a, iterator) + 1;

F - 見える数

問題文を理解するのに苦労する問題。iを固定すれば分かりやすい。例えば、入力例1においてi=2とした際に問題文の条件が成り立つかを確認する。それを全てのiについて繰り返し、条件を満たすiがいくつだったかを出力する。 （i=1の時にjが空集合になるので厳密には判断不可能だが、今回の場合は満たすものとするよう）

実装としては、数列の先頭から要素を見ていき、その際に今までの要素のうちの最大値を保持しておけば良い。

int answer = 0;
int maxNumber = 0;
REP(i,0,N) {
    if (maxNumber < a[i]) answer++;
    maxNumber = max(a[i], maxNumber);
}

G - あまり

数列を以下のように変形する。

1345 % MOD
= (1 * 10^3 + 3 * 10^2 + 4 * 10^1 + 5 * 10^0) % MOD
= ((((0 * 10 + 1) * 10 + 3) * 10 + 4) * 10 + 5) % MOD
= ((((0 * 10 + 1) % MOD * 10 + 3) % MOD * 10 + 4) % MOD * 10 + 5) % MOD

すると、「10倍する」「その桁の数字を足す」という作業を先頭の桁から順に繰り返せば良いことに気づく。これはfor文で簡単に実装できる。
あとは、計算途中で毎回1,000,000,007で割ることで、long longの範囲を超えないように気をつければ良い。

もちろん多倍長整数でも解ける。ただし、C++のboost/multiprecisionを愚直に使うだけではTLEしたが、pythonでやればギリギリ時間内に収まった。

H - LIS

LIS とは最長増加部分列(Longest Increasing Subsequence)のこと。

• 増加: 単調増加
• 部分列: 元の数列のうち一部の要素だけをピックアップして構成される数列。順番は崩してはいけないが、ピックアップする要素は連続していなくても良い。

DPを使えば解ける。典型的な方法では、dp[増加部分列の長さ] = 部分列の最終要素の最小値とすれば良い。最初は最小値をINFで初期化して、後述の更新手順を繰り返していって、最小値がINFじゃなくなったIndexのうち最大のIndexが答えになる。

更新手順は以下。

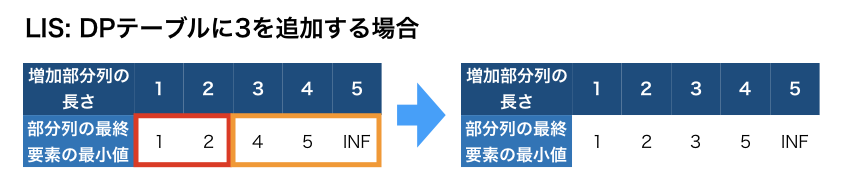
図はある時点でのDPテーブルの状態を示したもので、その状態から新たに「3」が使えるとした場合に、どのようにDPテーブルを更新するかを考える。

• 「3」より小さい部分（赤枠）について
  • 部分列に3より大きい数字が存在しないので置換できる要素が存在しない
  • （因みに部分列の後ろに加えるのは、部分列の長さが変わってしまうので駄目）
• 「3」より大きい部分（オレンジ枠）について
  • 長さ3の部分列は、4から3に置換できる
  • 長さ4の部分列は、長さ3の部分列の後ろに5を付け加えた部分列なので、3に置換できる箇所は最終より1つ前の要素（＝4）であり、最終要素は5のままとなる
  • 長さ5の部分列も同様に最終要素はそのまま

つまり、「3」より大きい最小値のうち最も左の最小値（＝4）を「3」に置換すれば良い。

fill(dp, dp + MAX_N, INF);

REP(i,0,N) {
    auto itr = upper_bound(begin(dp), end(dp), a[i]);
    *itr = a[i];
}

int answer = (int)distance(begin(dp), lower_bound(begin(dp), end(dp), INF));

I - 和がNの区間

連続した区間に関する問題で、しゃくとり法が使える。
まず、事前に累積和を求めておき、任意の連続した区間の和がすぐに求められるようにしておく。
探索の際には、探索対象区間の左端・右端を意味するleft, rightの2つのindexを持っておき、その区間の和がNより大きければ区間が広すぎるのでleftをインクリメント、小さければ区間が狭すぎるのでrightをインクリメント、等しければその区間を正解としてカウントした上でleft, rightをインクリメント、という手順を繰り返して探索対象区間を変化させていく。

int answer = 0, left = 0, right = 0;
while (right < N+1) {
    // sum[0] == 0
    int diff = sum[right] - sum[left];
    if (diff == N) {
        left++;
        right++;
        answer++;
    } else if (diff > N) {
        left++;
    } else {
        right++;
    }
}

J - 転倒数

スワップの発生回数は転倒数とも呼ばれ、i<jかつa_i > a_jとなる組の個数と同値となる（ソートされた数列に対して逆スワップを1回発生させると上記の組が1つずつ増えていくことから、直感的に理解できる）

上記の組の個数を求める方法は主に2つある（蟻本でも紹介されている）

BIT (Binary Indexed Tree)

BITとは、配列bに対して、累積和b_0 + b_1 + ... + b_iをO(log n)で求めるアルゴリズムである。

BITで転倒数を求めるには、b_iを、すでにその値を探索したかどうか、というフラグ（0だと未探索、1だと探索済み）として定義すれば良い。すると、探索済みの要素のうち、b_iより小さい要素の個数は累積和b_0 + b_1 + ... + b_{i-1}で求められる。

ll answer = 0;
BIT bit(N);
REP(i,0,N) {
    answer += i - bit.sum(a[i]);
    bit.add(a[i], 1);
}

ちなみにBITはセグメントツリーの機能制限版のようなものなので、セグメントツリーでも解ける

分割統治法

分割統治法は、数列を分割し、区間ごとに転倒数を再帰的に求めてそれをマージしていくアルゴリズムである。

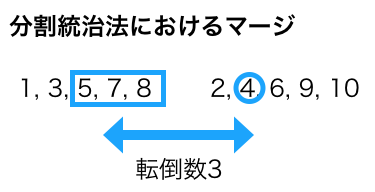
まず、数列を中央で分割し、左右それぞれで転倒数を再帰的に求める。
重要なのはそれをマージする方法で、マージする場合は左右で転倒している要素の数を求める必要がある。
図で説明すると、右に含まれている「4」より大きな要素が左に「5,7,8」の3つ存在するため、「4」に関連する転倒数は3である。このような計算を「2,6,9,10」に対しても繰り返して、それらを合計した数を足すことで、マージした際の転倒数が正しく求められる。
なお、この計算をすばやく行うために、マージする際には左右をそれぞれソートしておく必要がある。

実装はSpaghetti Source - バブルソートの交換回数を参考にする。

K - 辞書順で何番目？

問題文の「長さNの順列のうち」とは、 {1, 2, 3, 4, 5},...,{5, 4, 3, 2, 1}のN!通りの順列のうち、という意味である。

例として「35142」で考えてみる。

辞書順なので先頭から考えればよい。35142の一桁目は3なので「一桁目が1,2の順列」よりも後ろになる。「一桁目が1,2の順列」は2 * 4!通り。
次に、35142の二桁目は5なので、「一桁目が3かつ二桁目が4以下の順列」よりも後ろになる。ここで注意しなければいけないのが、二桁目のパターン数を考える際は既に使用した数は差し引いて考えることである。具体的に言えば、4以下の数は本来1, 2, 3, 4の4通りであるが、一桁目において3を既に使用しているため、二桁目のパターンは1,2,4の3通りとなり、「一桁目が3かつ二桁目が4以下の順列」は(4-1) * 3!通りとなる。

このように、辞書順を考える上では「iより小さい未使用の数字はいくつあるか」を各桁ごとに考える必要がある。この計算はJ問題と同じくBITが使える。つまり、長さNのBITを最初全て0で初期化し、使った数字については+1すれば、iまでの総和がそのまま使用済みの数字の数としてBITで簡単に計算できるため、未使用の数も簡単に計算できる。

ll answer = 0;
BIT bit(N);
REP(i,0,N) {
    // factorialは計算済みとする
    answer += ((A[i]-1) - bit.sum(A[i]-1)) * factorial[N-i-1];
    answer %= MOD;
    bit.add(A[i], 1);
}
answer += 1;
answer %= MOD;

L - N回スワップ

転倒数の応用問題のようだが、「任意の」ペアのスワップなのでバブルソートのスワップとは異なる。

スワップの方法としては、iがi番目に存在しなかった場合にi番目に持っていく、という操作をひたすら繰り返す。
基本的にはこの操作1回ごとに「正しく配置されている数字」が1つずつ増えていくが、1回の操作で2増えることもある（「1,2,4,3,5」の4と3を入れ替えるときなど）。ただ、上記の操作を繰り返す過程でこの3と4の位置に他の数字が入ってくることは無い。よって、スワップの順序によってスワップの回数が変化することはない。

そのようにして一度昇順に並び替えた後、同じ数字のペアをひたすらスワップすることで、転倒数とNの偶奇が一致するときのみ昇順に並び替えられる。

int swap = 0;
REP(i,0,N) {
    while (A[i] != i+1) {
        // swap
        int tmp = A[i];
        A[i] = A[tmp-1];
        A[tmp-1] = tmp;

        swap++;
    }
}
bool answer = (N - swap) % 2 == 0;